预防猝死
- boke
- 2024-05-21
- 5:57 下午
JACC | 高Lp(a)水平与易损斑块共存在时,心梗风险增加5倍
流行病学、遗传学和前瞻性队列研究提供了强有力的证据,表明脂蛋白(a)[Lp(a)]水平与心肌梗死(MI)风险有关。然而,Lp(a)水平升高,与MI风险之间的具体机制尚不明确。
斑块破裂是心肌梗死(MI)事件最常见的诱因。在组织学上,易损斑块特征包括一个富含脂质的大坏死核心和薄纤维帽,这些特征可以在冠状动脉计算机断层扫描血管造影(CCTA)中被检测为低衰减斑块(LAP)。
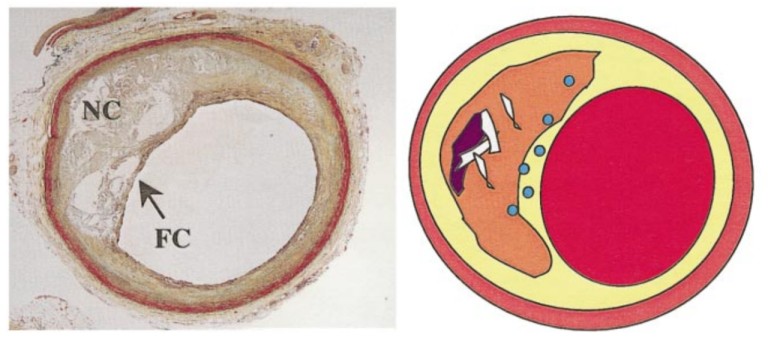
易损斑块[1]
既往研究表明,从CCTA获得的LAP是MI的独立预测因子,高浓度的血清Lp(a)加速了晚期稳定型冠状动脉疾病(CAD)患者LAP体积的进展。同时,斑块的进展,特别是不良斑块表型的进展,增加了斑块破裂的可能性,并导致随后的MI。然而,目前尚不清楚Lp(a)与MI风险之间的关联是否因LAP的存在而增强。
近期,JACC的一项多中心研究发现,Lp(a)升高与心梗风险增加之间的关系,可能与易损斑块有关[2]。
该研究首先前瞻性纳入5607例接受冠脉CT和Lp(a)检查、疑为冠心病的稳定性胸痛患者作为衍生队列,根据纳入标准,共有5,607名患者完成了8.2年的随访;此外,有1,122名患者完成了8.0年的随访,纳入到验证队列。Lp(a)升高定义为Lp(a) ≥50 mg/dL。
研究发现,随着Lp(a)水平的增加,LAP的发生率显著增加(Ptrend <0.001)(下图)。当Lp(a)设置为连续变量时,每增加50 mg/dL的Lp(a)使LAP存在风险增加2.7倍。此外,多变量线性回归分析表明,Lp(a)水平增加与LAP体积呈正相关。
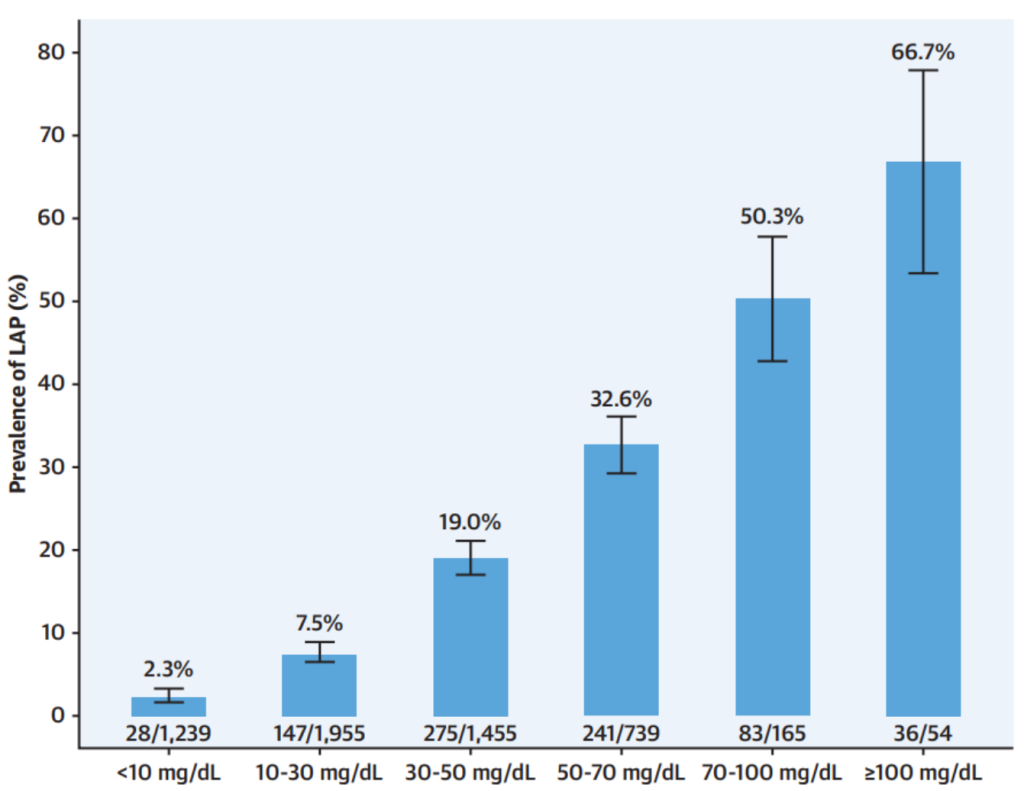
Lp(a)水平与LAP发生正相关[2]
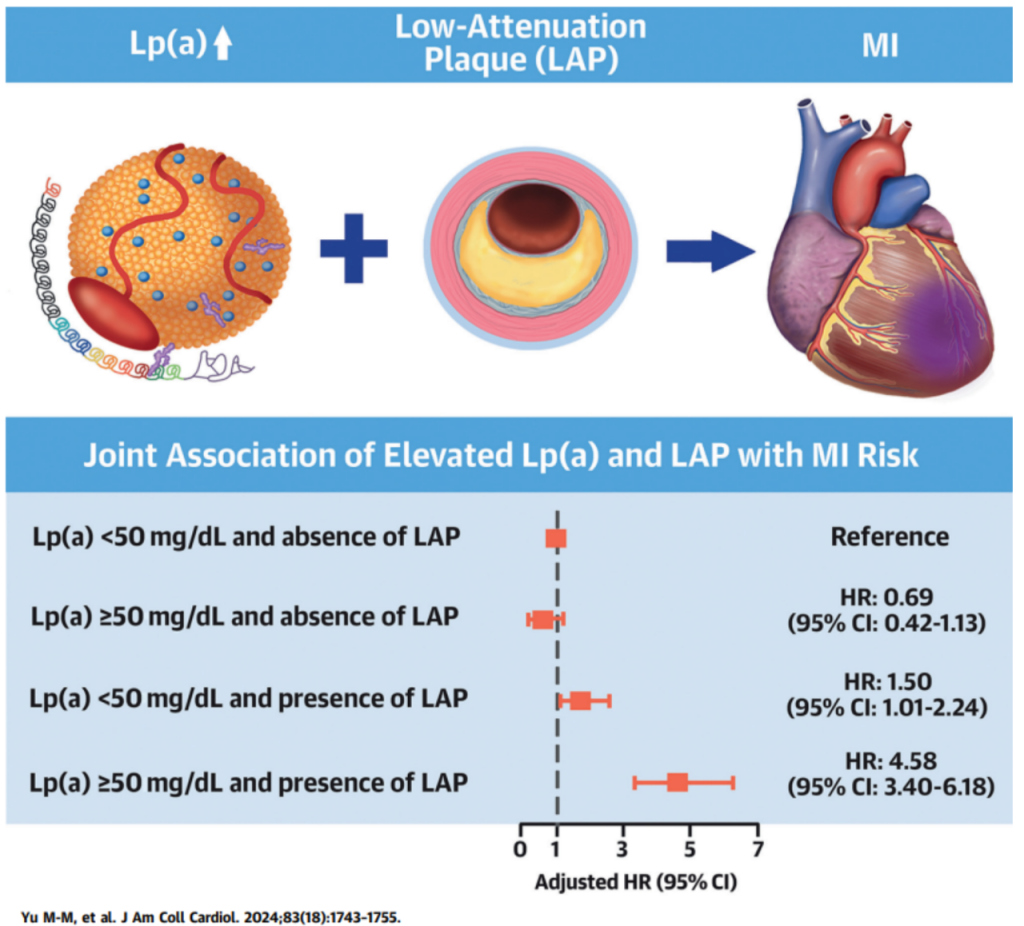
Lp(a)与LAP分层的MI方面,总体人群中Lp(a)升高患者的10年累积MI发生率是未升高患者的近2倍。在LAP存在的情况下,具有Lp(a)升高的患者的10年累积MI发生率明显高于那些没有Lp(a)升高的患者(26.1% vs 6.5%)。然而,在没有LAP的患者中,两组的10年累积发生率相似且较低(3.1% vs 4.6%)。
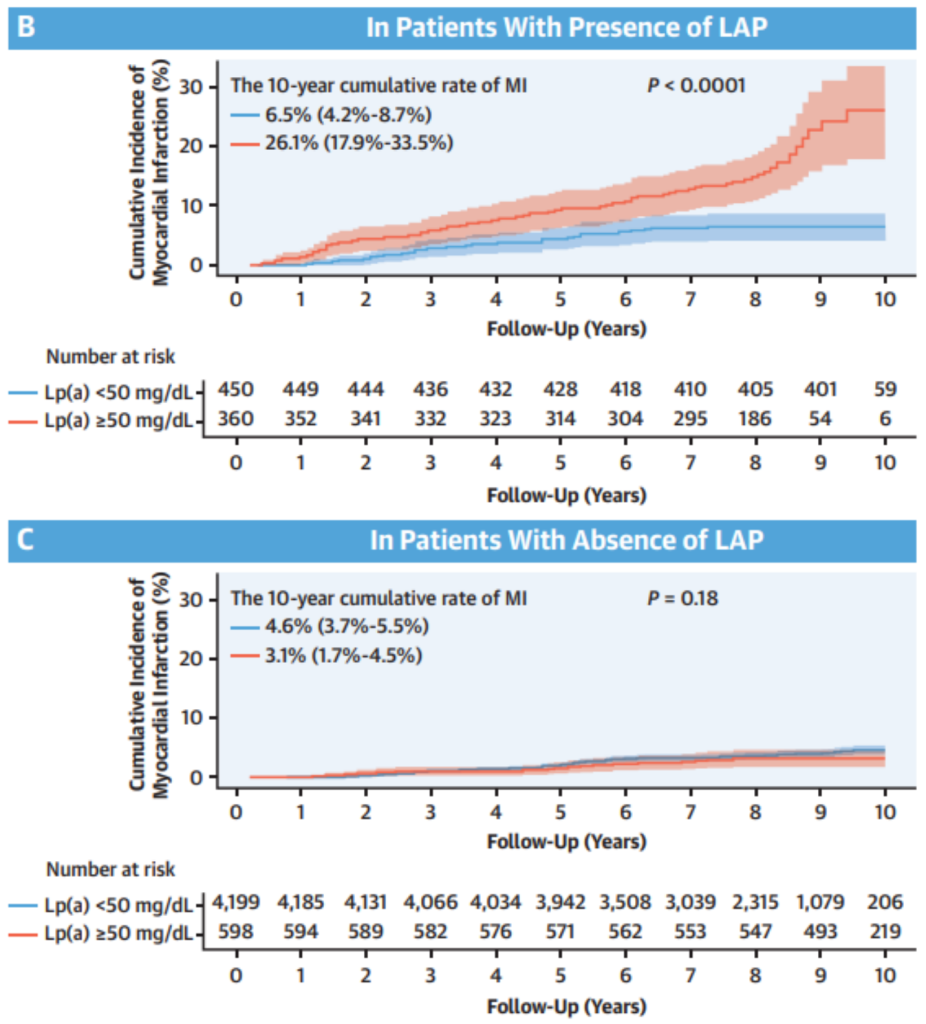
LAP分层下Lp(a)与MI的关联分析[2]
单核苷酸变异(SNV)和插入缺失 (INDEL)是基因组变异的常见形式,也是引起人类疾病的重要原因。
选取NA12878标准品,与预期SNV和INDEL变异进行比较。结果表明,在MGI与Illumina测序平台,SNP灵敏度为99.1%,INDEL灵敏度为91.6%。Lp(a)和LAP之间存在显著的相互作用。在具有LAP的患者中,经调整后的模型中,Lp(a)升高与MI风险显著相关(校正HR:3.03)。然而,在没有LAP的患者中,观察到Lp(a)与MI风险之间没有关联(校正HR:1.12)。在验证队列中也观察到了相同的结果。
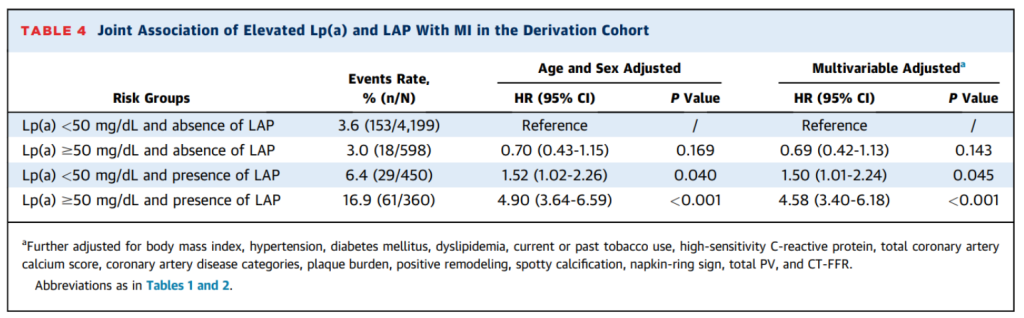
在多变量Cox回归中,这两个危险因素的共存与参考组(Lp[a] <50 mg/dL且没有LAP)相比,MI的风险约为其5倍(校正HR:4.58)(下表)。在验证队列中也观察到类似的结果(补充表7)。在推导队列中,中介分析显示,LAP的存在对Lp(a)与MI的关系具有显著的间接效应,并且对于Lp(a)与MI的关联贡献了73.3%。在验证队列中也有相似的结果。
研究人员推测,高水平的Lp(a)在坏死性斑块的形成和发展中可能起到不同的作用。在坏死性核心斑块的环境中,Lp(a)可能迅速刺激炎症细胞浸润到动脉壁中,导致坏死核心的增加,并减弱纤维帽。最终,这使得斑块易于破裂并引发MI。换句话说,高水平的Lp(a)主要增加了易损斑块破裂的风险。
通过该项多中心队列研究,发现了有关Lp(a)与MI发生的重要见解。当高Lp(a)水平与LAP的共存在时,MI的风险更高,这对于风险评估以及预防性治疗的使用具有重要意义。
参考资料
1. Virmani R, Kolodgie FD, Burke AP, Farb A,Schwartz SM. Lessons from sudden coronary death: a comprehensive morphological classification scheme for atherosclerotic lesions. Arterioscler Thromb Vasc Biol. 2000;20:1262–1275.
2. Yu M M, Wang M L, Wang J J, et al. Association of lipoprotein (a) levels with myocardial infarction in patients with low-attenuation plaque[J]. Journal of the American College of Cardiology, 2024, 83(18): 1743-1755.


